1. 활성화 함수
딥러닝을 수행할 때 각 뉴런은 입력받은 값을 바로 전달하지 않고 활성화 함수를 통과시킨 뒤 다음 뉴런으로 값을 전달한다. 활성화 함수는 비선형 함수이다.
아래 그림을 보자. 활성화 함수를 사용하지 않고 값을 그대로 전달하게 된다면 뉴런을 구성하고, hidden layer를 구성하는 의미가 없어진다.

또한 활성화 함수를 선형 함수로 한다면 아래와 같은 상황이 발생한다.
1) 1층 뉴런의 활성화 함수는 $h(x)= 2x+ 5$, 2층 뉴런의 활성화 함수는 $g(x)= -3x+ 2$이다.
2) 입력값 $x$가 1층-> 2충 뉴런을 거쳐 출력된다.
3) 따라서 출력은 $g(h(x))= -3(2x+ 5)+ 2= g(h(x))= -3(2x+ 5)+ 2= -6x -13$이다.
4) 이는 $h(x)=-6x-13$인 층 1개를 사용하는 것과 차이가 없다.
하나의 층으로는 다양한 문제를 해결할 수 없기 때문에 활성화 함수가 필요하고, 활성화 함수는 비선형 함수이다.
2. 로지스틱 함수(=sigmoid함수)

$$ h(z)= 1/(1h(z)= \frac{1}{(1+e^{-z})} $$
$0\leq h(z)\leq 1$의 값을 가진다.
모든 값에서 미분 가능하다.
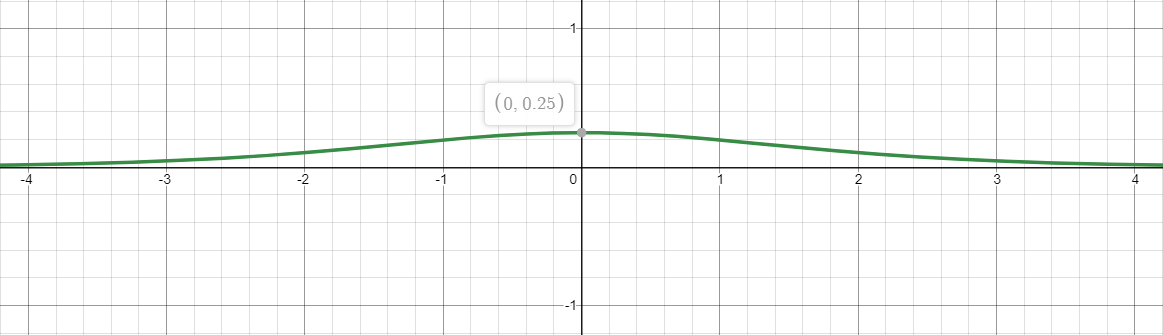
$$ \frac{\partial}{\partial z}h(z)= \frac{e^x}{(e^x+1)^2} $$
3. tanh

$$ h(z)= tanh(z) $$
$-1\leq h(z)\leq 1$의 값을 가진다.
모든 값에서 미분 가능하다.

$$\frac{\partial}{\partial z}h(z)= sech^2(z)$$
4. ReLU

$$h(z)=\left\{\begin{matrix}
z (z\geq 0)
\\
0 (z< 0)
\end{matrix}\right.$$
$z\geq 0$에서 미분 가능하다.
5. step

$$h(z)=\left\{\begin{matrix}
1 (z\geq 0)
\\
0 (z< 0)
\end{matrix}\right.$$
$z= 0$일 때 미분 불가능하다.
#################################
잘못된 내용 발견시 덧글 부탁드립니다.
#################################
<출처 및 참고자료>
[1] 오렐리앙 제롱. Hands-On Machine Learning with Scikit-Learn, Keras&Tensorflow 2판. 한빛미디어
<사용도구>
[1] 그래프 그리는 사이트
* ReLU, step function은 다수의 그래프를 합쳐 수정한 것임
www.desmos.com/calculator?lang=ko
Desmos | 그래핑 계산기
www.desmos.com
'딥러닝' 카테고리의 다른 글
| 파이토치에서 텐서보드 사용하기 (0) | 2021.06.15 |
|---|---|
| [논문리딩] YOWO(You Only Watch Once) (0) | 2021.01.25 |
| [번외] CPU와 GPU의 학습 속도 (0) | 2020.10.13 |
| 순전파/역전파 (0) | 2020.09.24 |
| 퍼셉트론 (0) | 2020.09.17 |
