본 포스팅은 CS231n의 3강 Loss Functions and Optimization을 정리한 내용입니다.
$f(x,W)$를 거쳐 나온 결과는 label갯수만큼의 점수를 가지며 이중 가장 점수가 높은 것을 결과로 출력한다.
여기서 $x$는 정해진 값이므로 결과는 $W$의 값에 따라 달라진다. 즉, 좋은 $W$를 찾는것이 최종 목적이라 할 수 있다.
이 때 현재 $W$가 좋은 값인지, 얼마나 잘못되었는지 정량화하여 알려주는것이 Loss function이다.
손실함수의 역할 : 현재 $W$가 얼마나 좋은지, 나쁜지 정량화
$$ L= 1/N\sum_{i}^{}L_{i}(f(x_{i},W),y_{i}) $$
각각의 label에 대해 loss를 구한다($L_{i}$) 이후 평군을 내 최종 $loss(L)$을 구한다
multiclass SVM loss

여기서 $s_{j}$는 해당 class의 분류결과이다.
모델 출력 $s_{j}$가 $s_{y_{i}} +1 (margen)$보다 작다면 0
loss가 0이라는건 모델이 잘 분류했다는 뜻이다.
여기서 숫자는 상대적 비교를 위한 값일 뿐 특정한 의미를 갖지 않는다.
예)

고양이 이미지(input)에 대해 loss를 계산하면 다음과 같다.
1) 모델은 input에 대해 $cat=3.2, car=5.1, frog=-1.7$의 결과를 출력했다.
2) 여기서 정답 class인 cat을 제외한 나머지 class(car, frog)값으로 각각 $max(0, s_{j}- s_{y_{i}}+ 1)$를 계산한다.
3) 계산된 결과를 더한다.
이를 이용해 고양이 사진이 입력됐을 때의 $L_{i}$는 2.9가 된다.
동일한 방법으로 모든 class의 loss를 계산한 뒤 평균을 취하면 모델의 최종 loss를 구할 수 있다.

여기서 구한 5.27이 $W$의 값이 얼마나 좋은지 정량적으로 나타낸 지표가 되며, 0에 가까울수록 성능이 좋다는 것을 의미한다.
regularization
모델 학습을 진행할 때 loss가 0이 되는것을 찾는데에만 집착하면 과적합이 발생할 수 있다. 학습은 train데이터에 대해서만 진행되기 때문이다.
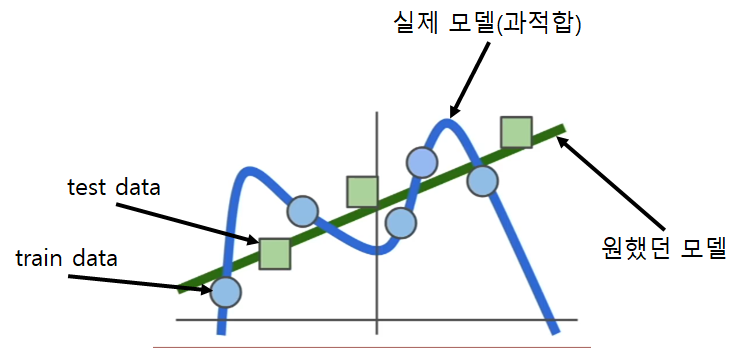
이러한 과적합 문제를 해결하는 방법을 regularization이라 한다.
$$ L(W)=1/N \sum_{i= 1}^{N}L_{i}(f(x_{i},W),y_{i})+\lambda R(W) $$
기존의 loss function에 $\lambda R(W)$가 추가되었는데, 이것이 regularization이며 "모델을 더 간단하게" 만드는 역할을 한다. 여기서 "모델을 더 간단하게"만드는 것은 모델이 조금 더 단순한 $W$를 선택하도록 돕는것을 의미한다.("단순"의 기준은 모델에 따라 다름)
즉, regularization은 모델이 train데이터에만 완벽하게 fit하지 않게 패널티를 부여하는 역할을 한다.
regularization의 종류

softmax classifier(multinomial Logistic Regression)
multiclass SVM loss에서 loss의 값은 상대적 비교시에만 의미가 있었고 score 자체에는 의미가 없었다. softmax classifier는 score 자체에 의미를 부여하고 수식을 이용해 확률분포를 계산한다.
$$ L_{i}= -log(\frac{e^{s_{y_i}}}{\sum _{j}e^{s_{j}}}) $$
softmax를 거치므로 모든 값은 해당 class의 확률이 된다.
여기서 log에 음수를 취하는데 loss란 "현재 weight가 얼마나 안좋은가"를 의미한다. 하지만 softmax를 거친 결과는 값이 클수록(여기서 값은 multiclass SVM과 달리 의미를 갖는다)좋다는 의미이기에 음수를 취한다.

optimization
최적의 weight를 구하는 것은 발의 촉감만을 이용해 산에서 가장 깊은 골짜기를 찾는것과 비슷하다.
미분을 통해 gradient를 구할 수 있고 gradiant에 음수를 취하면 얼마나 가파른지 알 수 있다.
실제로도 gradient를 이용해 최적화를 진행하고 있다.
weight 하나하나를 일일히 수치적으로 계산할 수 있으나 이는 비효율적이고, 시간도 오래걸린다.
그렇기에 실제 gradient를 구현할 때는 분석적인 방법을 이용한다.
gradient descent
while True:
weights_grad = evaluate_gradient(loss_fun, data, weights)
weights += -step_size * weights_grad1) weight를 임의의 값으로 초기화 한다.
2) loss와 gradient를 계산한 뒤 weight를 gradient의 반대 방향으로 업데이트 한다.
3) 이를 계속 반복하면 loss는 점점 작아져 최적의 값을 구할 수 있다.
weight를 업데이트 할 때 얼만큼 업데이트(이동)할지 정해주는 값을 learning rate라 하고, 이는 하이퍼파라미터이다.
stochastic gradient descent(SGD)
gradient descent를 계산할 때 데이터의 갯수가 매우 커진다 가성해보자.
$$ L(W)= \frac{1}{N}\sum_{i= 1}^{N}L_{i}(x_{i},y_{y},W)+\lambda R(W) $$
$$ \bigtriangledown wL(W)=\frac{1}{N}\sum_{i=1}^{N}\bigtriangledown wL_{i}(x_{i},y_{i},W)+\lambda \bigtriangledown wR(W) $$
이는 위 식에서 N이 커진다는 뜻이고 이는 하나의 gradient를 계산할 때 연산량이 매우 많아지고, 이는 속도가 매우 느려진다는 것을 의미한다.
그렇기에 실제로 사용할 때 stochastic gradient descent를 사용한다.
stochastic gradient descent 데이터를 mini batch로 나눠 train하는 것으로, mini batch를 이용해 loss전체합의 추정치와 실제 gradient의 추청치를 계산한다.
while True:
data_batch = sample_training_data(data, 256)
weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
weights += -stepsize * weights_gradSGD는 거의 모든 DNN알고리즘에 사용되는 기본적인 학습 알고리즘이다.
'딥러닝' 카테고리의 다른 글
| [CS231n] Lecture 2. Image Classification (0) | 2021.07.18 |
|---|---|
| 파이토치에서 텐서보드 사용하기 (0) | 2021.06.15 |
| [논문리딩] YOWO(You Only Watch Once) (0) | 2021.01.25 |
| [번외] CPU와 GPU의 학습 속도 (0) | 2020.10.13 |
| 순전파/역전파 (0) | 2020.09.24 |
